Answer:
0.002 mg of sample will be left after 40 days.
Explanation:
Half life of the iodine-131 =
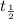 = 8 days
= 8 days
Initial amount of iodine-131 =
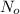 = 64 milligrams = 0.064 g
= 64 milligrams = 0.064 g
Amount of iodine-131 left after the time of 40 days = N
Decay constant =
 = ?
= ?
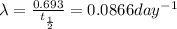
![\log[N]=\log[N_o]-(\lambda * t)/(2.303)](https://img.qammunity.org/2020/formulas/mathematics/high-school/j275b4gj5xhm9dbi46uj0tm7dga38r8z8c.png)
![\log[N]=\log[0.064 g]-(0.0866 day^(-1)* 40 days)/(2.303)](https://img.qammunity.org/2020/formulas/mathematics/high-school/l1qwjo0sdfeo9bsiasy8e1vedbe9ahjibs.png)
![N=Antilog [-2.6979 g]](https://img.qammunity.org/2020/formulas/mathematics/high-school/h1yecyxfumukgkjbnfmxcil2tawd7e8nve.png)
N = 0.002004 g = 0.002 mg
0.002 mg of sample will be left after 40 days.