Question

If 4a - 13 = 6b + 35 = 8c -17 = d, find the smallest possible value of a + b + c + d.

(they are integers)

Answer 1

The smallest possible value of a+b+c+d is: 4

Explanation:

since we are given that:

4a - 13 = 6b + 35 = 8c -17 = d

on taking the first two equality i.e. 4a-13=6b+35

we get
`b=(2)/(3)a-8`

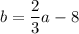
on using the first and third equality we have:

4a-13=8c-17

`c=(1)/(2)a+(1)/(2)`

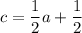
also from the first and last equality we have:

d=4a-13

Hence,

`a+b+c+d=a+(2)/(3)a-8+(1)/(2)a+(1)/(2)+4a-13\\\\a+b+c+d=(37a)/(6)-(41)/(2)`

`a+b+c+d=(37a-123)/(6)`

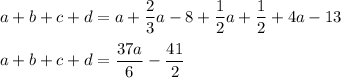
the smallest possible value such that the expression a+b+c+d is positive will be claculated as:

a+b+c+d>0

that means
`(37a-123)/(6)>0`

`a>3.324`

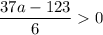
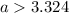
But as a is an integer, hence the smallest such value is 4.