Question

The number of butterfly gardens in a region, after x years, can be represented by the function G(x) = 5(1.05)x + 1. The approximate number of butterflies in each of these butterfly gardens, in hundreds, after x years, can be represented by the function B(x) = (1.05)8x. Which function best describes T(x), the total number of butterflies, in hundreds, in the butterfly gardens in this region, after x years?

Answer 1

Total No of Butter flies in region is
`5(1.05)^(9x+1)`.

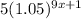Explanation:

No of Butterfly gardens in a region after x years , G(x) =
`5(1.05)^(x+1)`

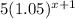
No of Butterflies in a garden after x years , B(x) =
`(1.05)^(8x)`

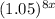
Total No of Butter flies in region , T(x) = G(x) × B(x)

T(x) =
`5(1.05)^(x+1)*(1.05)^(8x)`

=
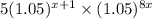
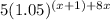`5(1.05)^((x+1)+8x)` (using law of exponent:
`x^a* x^b=x^(a+b)`)

=
`5(1.05)^(9x+1)`

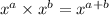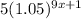
Therefore, Total No of Butter flies in region is
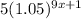`5(1.05)^(9x+1)`.