Question

A participant in a 21 mile walkathon walks at a steady rate of 3 miles per hour. He thinks "The relationship between the number of miles left to walk and the number of hours I already walked can be represented by a line with slope of -3." Do you agree with his claim? Explain your reasoning

Answer 1

`y=21-3h`

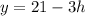
Yes, the participant is right.

Explanation:

Let h be the number of hours.

We have been that a participant in a 21 mile walkathon walks at a steady rate of 3 miles per hour. Then distance traveled in h hours will be 3h.

As the remaining distance is decreasing with each passing hour, so the remaining distance will be initial distance minus the distance covered in h hours. We can represent this information as:

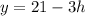`y=21-3h`, where y represents miles left to walk.

Since we know that slope-intercept form of an equation is:
`y=mx+b`, where,

m= Slope of the line.

b = y-intercept or initial value.

Upon comparing our equation with slope-intercept form of equation we can see that slope of our line is -3, therefore, the participant is right.

Answer 2

Answer: Yes, I do agree with the claim.

Step-by-step explanation: As shown in the attached figure, the participant walks a path of 21 miles at a speed of 3 miles/hour.

He started at point A and reached at point B after walking a distance of 'x' miles in some time. He takes another t hours to walk from point B to final point C. Distance from B to C is (21-x).

Therefore, we have for path BC

`\textup{speed}=\frac{\textup{distance}}{\textup{time}}\\\\\Rightarrow 3=(21-x)/(t)\\\\\Rightarrow 3t=21-x\\\\\Rightarrow x=-3t+21,` which is a straight line with slope -3.

Thus, the participant's claim was absolutely correct and I completely agree with the claim.