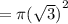ANSWER
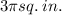
EXPLANATION
Let R be the radius of the bigger circle and r, be the radius of the smaller circle.
Then their ratio is given as,

We can rewrite it as fractions to get,
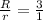
We make R the subject to get,
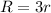
The area of the bigger circle can be found using the formula,
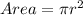
This implies that,
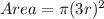
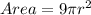
But it was given in the question that, the area of the bigger circle is 27π.
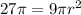
We divide through by 9π to get,
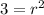
This means that,

The area of the smaller circle is therefore