Question

An isosceles triangle has angle measure 40, 40, and 100. The side across from the 100 angle is 10 inches long. How long are the other sides?

Answer 1

Answer: 6.53 Inches long

Explanation:

Welp. Just calculated it and got it right on a test, but I’m too lazy to explain. Just trust Tem!

Answer 2

The other two sides of given isosceles triangle are 6.53 inches long.

Explanation:

in the figure below,

ABC is an isosceles triangle has angle measure 40, 40, and 100. The side across from the 100 angle is 10 inches long an let this side be b

Let the other two be a inches long .

We have to find the measure of side AB.

Sine rule is an equation relating the lengths of the sides of a triangle to the sines of its angles. According to the law,

For a triangle Let B stands for the angle at B. Let C stand for the

angle at C and A for angle A. Also, let b = AC, a = BC and c = CB = a.

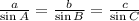`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)` ............(1)

Using sine rule,

Putting values in (1),

`(a)/(\sin 40)=(10)/(\sin 100)=(a)/(\sin 40)`

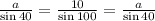
Considering first two ratios,

`(a)/(\sin 40)=(10)/(\sin 100)`

`{a}=(10 * \sin 40)/(\sin 100)`

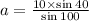
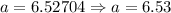`{a}=6.52704 \Rightarrow a=6.53`(approx)

Since, the triangle is isosceles so, other two sides are equal.

Thus, other sides are 6.53 inches long.