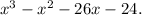Answer: The answer is (b)
Step-by-step explanation: We are given four polynomials and we are to check which one of them has roots -4, -1 and 6. Obviously, if putting these three values of 'x' in a polynomials yields 0, then that particular value will be a root of that polynomial.
Let us denote the polynomials as follows -
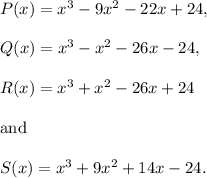
Let us check for x = -1 first. So, substituting x = -1 in all the four polynomils, we get
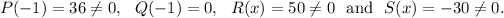
Therefore, only possibility is Q(x).
If we put x = -4 and x = 6 in Q(x), we find that

Thus, the correct option is (b)