Answer:
0.298
Explanation:
A company wanted to determine what percentage of its employees stayed for at least 1, 2, and 3 years.
The data they compiled is given below and covers 200 male employees and 300 female employees.
Male
1 year = 0.67
2 year = 0.45
3 year = 0.20
Female
1 year = 0.73
2 years = 0.64
3 years = 0.39.
Let A be the event that a male employee stayed at least 3 years
So,P(A) = 0.20
Let B be the event that they stayed 1 year
So, P(B) = 0.67
Now we are supposed to find the probability that a male employee stayed at least 3 years given that they stayed 1 year
So, the probability that a male employee stayed at least 3 years given that they stayed 1 year =
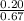
=
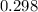
Hence the probability that a male employee stayed at least 3 years given that they stayed 1 year is 0.298.