Question

The box plots compare the number of calories in each snack pack of crackers and cookies.

Answer 1

The fourth Answer.

Explanation:

Answer 2

4th statement is true.

Step-by-step explanation:

We have been two box plots, which represents the number of calories in each snack pack of crackers and cookies. We are asked to find the correct statement about our given box plots.

1. More packets of crackers have 80 calories than any other number of calories.

We can see that median of box plot representing calories of cookies is 80. This means that half of the packets of crackers have less than 80 calories and half of the packets have more than 80 calories, therefore, 1st statement is false.

2. The value 70 is an outlier for the number of calories in the cookie pack.

Since an outlier is 1.5 times the interquartile range.

`IQR=Q_3-Q_1`

`\text{IQR of cookie packs}=105-90`

`\text{IQR of cookie packs}=15`

`\text{Lower outlier}=Q_1-(1.5*IQR)`

`\text{Lower outlier}=90-(1.5*15)`

`\text{Lower outlier}=90-22.5`

`\text{Lower outlier}=67.5`

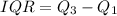
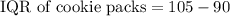
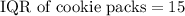
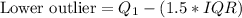
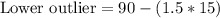
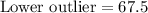
Since any number less than 67.5 will be an outlier and 70 is grater than 67.5, therefore, 70 is not an outlier in number of calories in cookie packs and 2nd statement is false.

3. The upper quartile of the cookie data is equivalent to the maximum in the cracker data.

We can see that upper quartile of cookie data is 105 and the maximum in cracker data is 100. Since 105 is greater than 100, therefore, 3rd statement is false.

4. The number of calories in each pack of cookies has a greater variation than the number of calories in each pack of crackers.

Since range and IQR are good measures of variation of box-plots, so we will find the range and IQR of our both box-plots.

We have already seen that IQR of cookie packs is 15.

`\text{IQR of cracker packs}=85-75`

`\text{IQR of cracker packs}=10`

`\text{Range}=\text{Maximum value - Minimum value}`

`\text{Range of calories in cracker packs}=100-70`

`\text{Range of calories in cracker packs}=30`

`\text{Range of calories in cookie packs}=115-70`

`\text{Range of calories in cookie packs}=45`

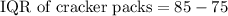
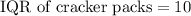
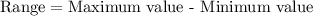
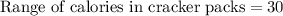
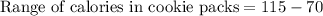
We can see that the range of calories in cookie packs (45) is greater than range of calories in cracker packs (30) and IQR of calories in cookie packs (15) is greater than IQR of calories in cracker packs (10), therefore, 4th statement is true.