Question

In a certain city, the hourly wage of workers on temporary employment contracts is normally distributed. The mean is $15 and the standard deviation is $3. What percentage of temporary workers earn less than $12 per hour?

Answer 1

Answer: B. 16%

Step-by-step explanation: I got this right on Edmentum

Answer 2

15.87%

Explanation:

We have been given that in a certain city, the hourly wage of workers on temporary employment contracts is normally distributed. The mean is $15 and the standard deviation is $3.

Let us find the z-score of 12, using z-score formula.

`z=(x-\mu)/(\sigma)`, where,

`z` = z-score,

`x` = Random sample score,

`\mu` = Mean,

`\sigma` = Standard deviation.

Upon substituting our given values in z-score formula we will get,

`z=(12-15)/(3)`

`z=(-3)/(3)`

`z=-1`

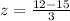
Let us find P(z<-1) using normal distribution table.

`P(z<-1)=0.15866`

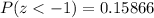
Therefore, probability of a temporary worker earns less than $12 per hour is 0.15866. Let us convert our given probability in percentage by multiplying by 100.

`\text{The percentage of temporary workers earn less than \$12 per hour}=0.15866* 100`

`\text{The percentage of temporary workers earn less than \$12 per hour}=15.866\approx 15.87`

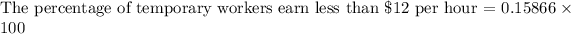
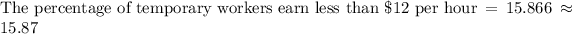
Therefore, 15.87% of temporary workers earn less than $12 per hour.