Answer:
79 balls.
Explanation:
We have been given that the weight of a basketball is normally distributed with a mean of 17 oz and a standard deviation of 2 oz.
Let us find the z-score for the weight 19 oz.

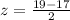
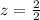
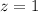
Let us find P(z>1) using normal distribution table.
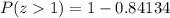
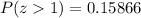
So the probability of a basketball having weight more than 19 oz is 0.15866. As there are 500 basketballs in the warehouse, so the total number of basketballs having a weight more than 19 oz will be:
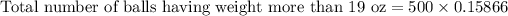
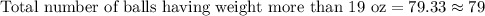
Therefore, 79 balls weigh more than 19 oz.