Question

B. Determine the mass of the sun

C. The sun is about 1000x farther from the Earth than the Moon, but it exerts a force on the Earth that is 100x greater than the force that the Moon exerts on the Earth. Explain how this is possible.

Please help!

Answer 1

B.
`1.99\cdot 10^(30) kg`

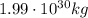
Step-by-step explanation:

The gravitational force between the Earth and the Sun is given by:

`F=G(Mm)/(r^2)`

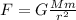
where

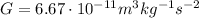`G=6.67\cdot 10^(-11) m^3 kg^(-1) s^(-2)` is the gravitational constamt

M is the mass of the Sun

`m=5.98\cdot 10^(24) kg` is the mass of the Earth

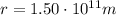`r=1.50\cdot 10^(11) m` is the distance between Earth and Sun

Since we know the magnitude of the gravitational force between Earth and Sun,
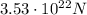`3.53\cdot 10^(22) N` (from the table given), we can re-arrange the formula and find the mass of the Sun, M:

`M=(Fr^2)/(Gm)=((3.53\cdot 10^(22)N)(1.50\cdot 10^(11) m)^2)/((6.67\cdot 10^(-11))(5.98\cdot 10^(24) kg))=1.99\cdot 10^(30) kg`

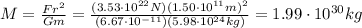
C. Because the mass of the Sun is much much greater than the mass of the Moon

Step-by-step explanation:

We already know the gravitational force between Earth and Sun (
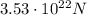`3.53 \cdot 10^(22) N`. By applying the same formula as before, we can calculate the gravitational force between Earth and Moon:

`F=G(Mm)/(r^2)`

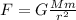
where

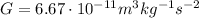`G=6.67\cdot 10^(-11) m^3 kg^(-1) s^(-2)` is the gravitational constamt

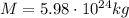`M=5.98\cdot 10^(24) kg` is the mass of the Earth

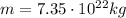`m=7.35\cdot 10^(22) kg` is the mass of the Moon

`r=3.84\cdot 10^(8) m` is the distance between Earth and Moon

Substituting into the formula, we find

`F=((6.67\cdot 10^(-11))(5.98\cdot 10^(24) kg)()7.35\cdot 10^(22) kg))/((3.84\cdot 10^8 m)^2)=1.99\cdot 10^(20) N`

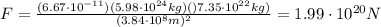
And we see that this is smaller than the force exerted by the Sun.