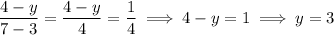"Rate of change" is a measure of how much some dependent variable changes with respect to a change in the independent variable. Given a function
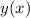 , the average rate of change over some interval
, the average rate of change over some interval
![[a,b]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x9eybysx3cihgn4xxsxk4fl3z5dcnyp7ww.png) is given by what's called the difference quotient,
is given by what's called the difference quotient,
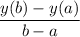
If
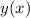 is a linear function, then the average rate of change is constant regardless of the interval chosen.
is a linear function, then the average rate of change is constant regardless of the interval chosen.
A line represents a linear function. The slope of the line represents the linear function's rate of change. We pick any two points on the line,
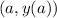 and
and
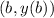 where
where
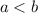 , and the slope of the line through them is exactly the value of the expression above. Then there are 3 possible scenarios:
, and the slope of the line through them is exactly the value of the expression above. Then there are 3 possible scenarios:
(1) If
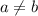 , then the slope can be any real number. If
, then the slope can be any real number. If
 happens to be true, then the slope is 0 and the line is horizontal.
happens to be true, then the slope is 0 and the line is horizontal.
(2) If
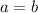 and
and
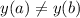 , the slope is undefined (some might say infinite) and the line is vertical.
, the slope is undefined (some might say infinite) and the line is vertical.
(3) If
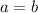 and
and
 , then we're talking about just one point. But there are infinitely many possible lines through a single point, so the slope is undefined.
, then we're talking about just one point. But there are infinitely many possible lines through a single point, so the slope is undefined.
Some examples in practice:
23. The slope of the line through (-5, 0) and (-5, 5) is
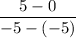
The
 -coordinates match but the
-coordinates match but the
 -coordinates don't, so this line is vertical and the slope is undefined (or infinite).
-coordinates don't, so this line is vertical and the slope is undefined (or infinite).
27. The slope is
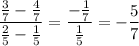
Notice the order in which we plug in the given points' coordinates. Always take
 to be the lesser of the two points'
to be the lesser of the two points'
 -coordinates! The convention is to always take points left to right.
-coordinates! The convention is to always take points left to right.
We use the same principles to work backwards:
31. Given a slope of 1/4 through two points (7, 4) and (3, y), we have