Answer:
The store mixes 8 pounds of peanuts and 9 pounds of raisins.
Explanation:
Let the store mixes 'x' pounds of peanuts and 'y' pounds of raisins.
The cost of peanut per pound is $3.20 and cost of raisins per pound $2.10
According to question,
Total weight of mixture given is 17 pounds.
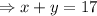 ................(1)
................(1)
also total cost of mixture given is $44.50
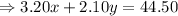 ...........(2)
...........(2)
Solving for equation (1) and (2),
Multiply equation (1) by 3.20 , we get
(1)⇒
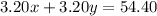 ............(3)
............(3)
Now, subtract equation (3) from equation (2) , we get

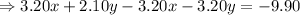
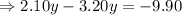
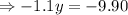
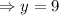
Thus, The store mixes 9 pounds of raisins.
Put, y = 9 in (1),
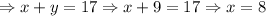
Thus, The store mixes 8 pounds of peanuts.