Answer:
The greatest common factor is 5x²
Explanation:
Step 1 : To find the greatest common factor, break down every term of both the polynomials into prime factors
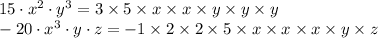
Step 2 : Now find the common factors which are common in both the polynomials
Common factors are : 5 , x and x
Step 3 : To find the greatest common factor find product of all the common factors obtained in the previous step
Greatest Common Factor = 5 × x × x
= 5·x²
So, The blanks will be : [5] x[2] y[0]