Question

Where do I start with this? it is a calc question. I thought perhaps relating the height to the length to get everything in terms of one variable by setting both legs to equal the hypotenuse with the Pythagorean theorem but I'm having trouble. dunno if that's even a good way of going about it.

Answer 1

See below.

Explanation:

You are correct in your approach. You can calculate the hypotenuse via Pythagoras, so you will know |AB|.

Then, I would do the following:

Denote the upper left corner of the rectangle that intersects with AB, a point D. Then call "a" the distance |AD|. Call the rectangle height x, and width y.

Use triangle similarity to set up a system of equations: A choice of "a" induces a rectangle x-by-y where

`(x)/(a)=(|BC|)/(|AB|)\implies x = (|BC|)/(|AB|)\cdot a\\(y)/(|AB|-a)=(|AC|)/(|AB|)\implies y = (|AC|)/(|AB|)\cdot (|AB|-a)=|AC|-(|AC|)/(|AB|)\cdot a`

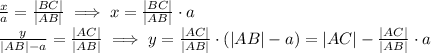
Now, we can get 2*(x+y) (aka, the perimeter) from those two equations:

`2(x+y)=2((|BC|)/(|AB|)\cdot a+|AC|-(|AC|)/(|AB|)\cdot a)=2a(|BC|-|AC|)/(|AB|)+2|AC|`

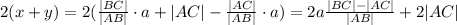
which is a function of one variable "a" and you can minimize that using a derivative.

But here's where I am finding this problem not a very good one: as you surely noticed the perimeter is linear in "a." As such, it's derivative will be constant and uninteresting. Even without the derivative you can see that to minimize the perimeter expression above, you should minimize "a." In other words "a" should become infinitesimal and the rectangle will be basically (epsilon) by (|AC|-epsilon), where epsilon is as small as possible.

I imagine this problem would become only then "interesting" (in that a derivative would give you something), if the question was to minimize the area of the rectangle.

Please feel free to let me know if you have questions.