Answers:
- b = -19
- b = -11
- b = -9
- b = 19
- b = 11
- b = 9
====================================================
Step-by-step explanation:
Here are all the ways to multiply to 18 when using integers only:
- -1*(-18) = 18
- -2*(-9) = 18
- -3*(-6) = 18
- 1*18 = 18
- 2*9 = 18
- 3*6 = 18
Sum each pair of factors to find out a possible value of b.
- -1 + (-18) = -19
- -2 + (-9) = -11
- -3 + (-6) = -9
- 1 + 18 = 19
- 2 + 9 = 11
- 3 + 6 = 9
Therefore, the possible values of b are
- b = -19
- b = -11
- b = -9
- b = 19
- b = 11
- b = 9
which are the final answers.
----------------------
An example:
Let's say b = 11. This would mean
 becomes
becomes
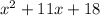
It would factor to
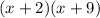 since it was stated earlier that:
since it was stated earlier that:
2+9 = 11
2 * 9 = 18
You can use the FOIL rule, distributive property, or the box method to confirm that
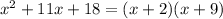 is a true equation for all real numbers x.
is a true equation for all real numbers x.
This same idea applies for the other values of b.
----------------------
If you're curious why this works, consider multiplying the two factors (x+p) and (x+q)
Use the FOIL rule to get
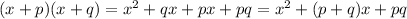
The middle term
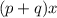 has the components add to the coefficient, while those same two components multiply to get the last term. This is why when factoring we're looking for two numbers that multiply to 18, and also add to the value of b (which in the case of the last example was 11).
has the components add to the coefficient, while those same two components multiply to get the last term. This is why when factoring we're looking for two numbers that multiply to 18, and also add to the value of b (which in the case of the last example was 11).