Question

Which exponential equation is equivalent to this logarithmic equation? log x = 4

Answer 1

To convert 'log x = 4' to an exponential equation, rewrite it as 'x = 10^4' which further simplifies to 'x = 10000'.

Step-by-step explanation:

To convert the logarithmic equation log x = 4 into an equivalent exponential equation, you use the fact that logarithms and exponentials are inverse functions.

Recall that the common logarithm (log) is the power to which 10 must be raised to obtain the number. So if log x = 4, it means that 104 = x. This is because when the common logarithm of a number is given, it implies a base of 10.

Hence, the exponential form of log x = 4 is x = 104 or 10000.

Answer 2

`x=10^(4)`

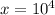
Step-by-step explanation:

Switching from Logarithmic to Exponential form:

An exponential base is the inverse of a logarithm with the same base. Given the equation log x = 4, note that the base of the logarithm isn't written in (it has no subscript). By default, the base of the logarithm function is base-10. So, to rewrite the equation using an exponential, we need to undo the logarithm with an exponential of the same base.

`\log(x)=4`

`10^{\log{(x)}}=10^(4)`

`x=10^(4)`

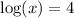
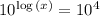
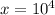
Analogies with Addition/Subtraction

Think about the equation x + 7 = 10.

I could tell you this is the equation in "addition form". What if I asked you to write an equation in "subtraction form"? While neither "addition form" nor "subtraction form" have been defined explicitly, one could undo the addition, and get an equation with subtraction in it, which one could argue is a "subtraction form" of the equation.

`x+7=10`

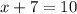
Subtracting 7 from both sides to undo the addition...

`(x+7)-7=(10)-7`

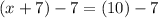
Simplifying the left side since the "+7" and "-7" cancel...

`x=10-7`

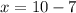
This is arguably in a "subtraction form" (there's a subtraction in it), whereas the original equation had addition in it.

While we could simplify this particular equation's right-hand side, we might not always be able to (what if the 10 had been a "y"... then the "y" and the "7" aren't like terms, and they would have to remain separate)

Similarly, in the logarithm problem, one could simplify 10^4 (it's 10,000), but one doesn't have to, and one won't always be able to.

For the logarithm problem, x=10^4 is the exponential form, as requested.