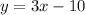Question

Which equation satisfies all three pairs of a and b values listed in the table?

a
b
0 -10
1 -7
2 -4

Answer 1

`y=3x-10\\`

Explanation:

An equation that satisfies all the values of a and b as listed is equation of line that passes through points A (0,-10), B (1,-7) and C (2,-4).

To understand this, first of all find points on a graph and connect the points. The result is a straight line passing through A, B and C.

The equation of straight line is given by:

`y= mx +b\\`

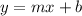
where m is slope of line and b is the y-intercept.

The slope of a line is given as :

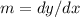`m= dy / dx\\` where dy is change in y and dx is change in x.

To find slope consider any two points from line. Let us consider A and C for this example. A(0,-10) is starting point of line and C (2,-4) is ending point of line ( we can also consider C as start point. It simply depends on choice).

Therefore, m= -4 -(-10) / 2-0 = -4+10/2= 6/2=3

Slope m= 3

On substituting value of m into equation.

`y= 3x +b\\`

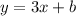
To find b, take any point A, B or C and simply put the value of y and x into the equation. We do this as A , B and C are simply solutions of the equation and thus can be used.

Taking C and substituting values:

-4= 3*2 + b

b=-10

The resultant equation is as follows:

`y= 3x -10\\`

Answer 2

`y = 3x -10`

Explanation:

The function seems to increase at a constant rate of 3 units. This means that the equation that satisfies these points could be that of a straight line.

We use the first two points to find the slope of the line.

(0, -10)

(1, -7)

(2, -4)

The equation of a line is:

`y = mx + b`

Where m is the slope of the line and b is the cutoff point with the y axis.

To find the slope of a line we use the following equation:

`m = (y_2-y_1)/(x_2-x_1)\\\\m = (-7 - (- 10))/(1-0)`

`m = 3`

So:

`y = 3x + b`

The cut point (b) is found by replacing in the previous equation, any of the three points provided and clearing b.

`-7 = 3(1) + b`

`b = -10`

Now we can write the equation of the line sought.

`y = 3x -10`

You can verify that the three points provided belong to this equation.