Answer: 258
Explanation:
Since, the sum of GP is,
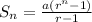
where r is the common ratio,
a is the first term,
n is the number of term,
Here, series is, 6, -12, 24, -48, _ _ _ _
Which is a GP ( Because there is common ratio in the given consecutive terms )
So, for the above series, a = 6, r =
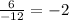 and n = 7,
and n = 7,
⇒

⇒
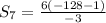
⇒
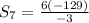
⇒
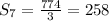
Thus, the sum of the 7 terms of the given series is 258.