Question

Identify the​ vertex, the axis of​ symmetry, the maximum or minimum​ value, and the range of the parabola for y=x^2+6x+13

Answer 1

Explanation:

First we can determine the x value of our vertex via the equation:

`x=(-b)/(2a)`

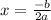
Note that in general a quadratic equation is such that:

`ax^2+bx+c`

In this case a,b and c are the coefficients and so a=1, b=6 and c=13.

Therefore we can determine the x component of the vertex by plugging in the values known and so:

`x=(-b)/(2a)=(-6)/(2(1))=(-6)/(2)=-3`

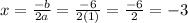
Now we can determine the y-component of our vertex by plugging in the x-component to the equation and so:

`f(x)=x^2+6x+13\\\\f(-3)=(-3)^2+6(-3)+13\\\\f(-3)=4`

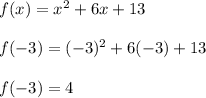
Therefore our vertex is (-3,4). Now in vertex our x component determines is the axis of symmetry so the equation for axis of symmetry is:

x=-3

Similarly, the y-component of our vertex is the minimum or maximum. In this case it is the minimum you can determine this because a is positive meaning that the parabola will point up, and so the equation for the minimum is:

y=4

The range of the formula is the smallest y-value meaning the minimum y=4 and all real numbers that are more than 4, mathematically:

Range = All real numbers greater than or equal to 4.