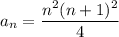Let
 denote the given sequence.
denote the given sequence.
 has forward differences
has forward differences
{9 - 1, 36 - 9, 100 - 36, ...} = {8, 27, 64, ...} = {2^3, 3^3, 4^3, ...}
If we call the sequence of forward differences
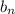 , then for
, then for
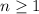 ,
,

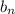 is defined in terms of
is defined in terms of
 for all
for all
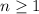 by
by
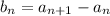
and so
 is defined recursively by
is defined recursively by
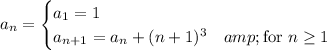
We can deduce a pattern for the general
 -th term:
-th term:
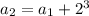
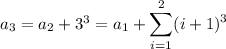
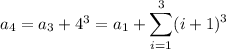
and so on, up to
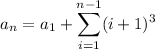
We can simplify the right hand side a bit, noticing that
 matches
matches
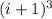 for
for
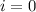 :
:
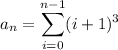
and to simplify things a bit more, we shift the index of summation:
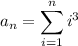
You should know that the right side has a nice closed form (look up "Faulhaber's formula" if you don't):