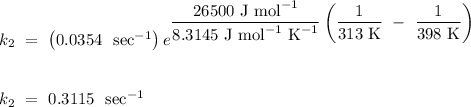Answer:
The rate constant of the reaction at 125˚ is
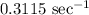 .
.
Step-by-step explanation:
The Arrhenius equation is a simple equation that describes the dependent relationship between temperature and the rate constant of a chemical reaction. The Arrhenius equation is written mathematically as
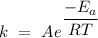
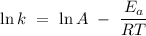
where
 is the rate constant,
is the rate constant,
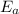 represents the activation energy of the chemical reaction,
represents the activation energy of the chemical reaction,
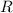 is the gas constant,
is the gas constant,
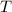 is the temperature, and
is the temperature, and
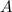 is the frequency factor.
is the frequency factor.
The frequency factor,
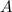 , is a constant that is derived experimentally and numerically that describes the frequency of molecular collisions and their orientation which varies slightly with temperature but this can be assumed to be constant across a small range of temperatures.
, is a constant that is derived experimentally and numerically that describes the frequency of molecular collisions and their orientation which varies slightly with temperature but this can be assumed to be constant across a small range of temperatures.
Consider that the rate constant be
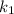 at an initial temperature
at an initial temperature
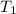 and the rate constant
and the rate constant
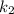 at a final temperature
at a final temperature
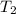 , thus
, thus

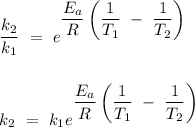
Given that
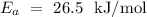 ,
,
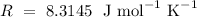 ,
,
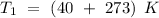 ,
,
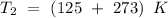 , and
, and
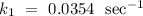 , therefore,
, therefore,