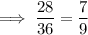Question

From a piece of tin in the shape of a square 6 inches on a side, the largest possible circle is cut out. What is the ratio of the area of the circle to the original square?

Answer 1

`\sf (1)/(4) \pi \quad or \quad (7)/(9)`

Explanation:

The width of a square is its side length.

The width of a circle is its diameter.

Therefore, the largest possible circle that can be cut out from a square is a circle whose diameter is equal in length to the side length of the square.

Formulas

`\sf \textsf{Area of a square}=s^2 \quad \textsf{(where s is the side length)}`

`\sf \textsf{Area of a circle}=\pi r^2 \quad \textsf{(where r is the radius)}`

`\sf \textsf{Radius of a circle}=(1)/(2)d \quad \textsf{(where d is the diameter)}`

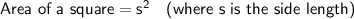
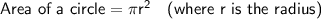
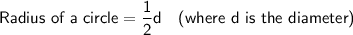
If the diameter is equal to the side length of the square, then:

`\implies \sf r=(1)/(2)s`

Therefore:

`\begin{aligned}\implies \sf Area\:of\:circle & = \sf \pi \left((s)/(2)\right)^2\\& = \sf \pi \left((s^2)/(4)\right)\\& = \sf (1)/(4)\pi s^2 \end{aligned}`

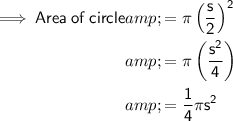
So the ratio of the area of the circle to the original square is:

`\begin{aligned}\textsf{area of circle} & :\textsf{area of square}\\\sf (1)/(4)\pi s^2 & : \sf s^2\\\sf (1)/(4)\pi & : 1\end{aligned}`

Given:

• side length (s) = 6 in
• radius (r) = 6 ÷ 2 = 3 in

`\implies \sf \textsf{Area of square}=6^2=36\:in^2`

`\implies \sf \textsf{Area of circle}=\pi \cdot 3^2=28\:in^2\:\:(nearest\:whole\:number)`

Ratio of circle to square:

`\implies (28)/(36)=(7)/(9)`