Explanation;
Mass of both the bullets = 0.11 g = 0.00011 kg
The length of pistol's barrel in meters= L
The length of rifle's barrel in meters= l
Exit speed of the bullet from pistol :
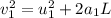
 (bullet was initially at rest)
(bullet was initially at rest)
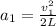
Force on the bullet by the pistol
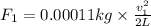 ..(1)
..(1)
Exit speed of the bullet from Riffle :

 (bullet was initially at rest)
(bullet was initially at rest)

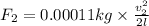 ..(2)
..(2)
Given
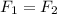
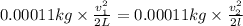
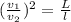
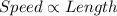
From this we can say that speed of the bullet is directly related to the length of the barrel of the firearm.
The higher speed of the bullet from riffle means that barrel length of the riffle is longer in which bullet is accelerated through longer distance.The longer length of riffles barrel explains the higher speed of the bullet when shot from the riffle.