Question

There are eight students in a class. Only one of them has passed Exam P/1 and only one of them has passed Exam FM/2. No student has passed more than one exam. What is the probability that exactly three students from a randomly chosen group of four students have not passed Exam P/1 or Exam FM/2?

Answer 1

Answer: There is probability of 0.57 chances that exactly three students from a group of four students have not passed Exam P/1 or Exam FM/2.

Explanation:

Total number of students = 8

Number of student who has passed Exam P/1 = 1

Number of student who has passed Exam FM/2 = 1

No student has passed more than one exam.

According to question, exactly three students from a randomly chose group of four students have not passed Exam P/1 or Exam FM/2.

So, Probability will be

`(^6C_3* ^2C_1)/(^8C_4)\\\\=(20* 2)/(70)\\\\=(4)/(7)\\\\=0.57`

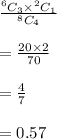
Hence, there is probability of 0.57 chances that exactly three students from a group of four students have not passed Exam P/1 or Exam FM/2.