Question

A bus started from rest with a uniform acceleration of 2m/s. A mate who is 9m behind the bus runs after it immediately with a uniform speed of 6m/s. calculate the time taken for the mate to draw level with the rear of the bus.

Answer 1

The bus's position
`x` at time
`t` is

`x_(\rm bus)=\frac12\left(2\,(\rm m)/(\rm s^2)\right)t^2`

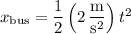
If we take the bus's rear's starting position to be the origin, then the position of the mate (?) is given by

`x_(\rm mate)=-9\,\mathrm m+\left(6\,(\rm m)/(\rm s)\right)t`

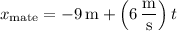
The mate draws level with the rear of the bus when
`x_(\rm bus)=x_(\rm mate)`:

`\frac12\left(2\,(\rm m)/(\rm s^2)\right)t^2=-9\,\mathrm m+\left(6\,(\rm m)/(\rm s)\right)t`

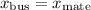Drop the units to make things simpler:

`\frac22t^2=-9+6t\iff t^2-6t+9=(t-3)^2=0\implies t=3`

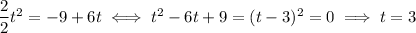
So it would take 3 seconds for the mate to catch up to the bus.