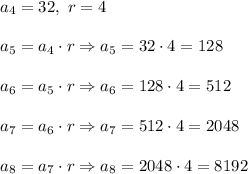Geometric sequence.
A geometric sequence goes from one term to the next by always multiplying or dividing by the constant value except 0. The constant number multiplied (or divided) at each stage of a geometric sequence is called the common ratio (r).
We have:
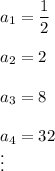
Find the common ratio:
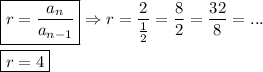
The formula of the n-th term of a geometric sequence:
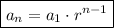
Substitute:
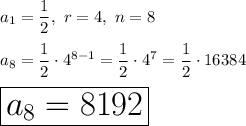
Method step by step: