Answer:
Local maximum is at 2007
Explanation:
Given the table which shows the number of members belonging to a community volunteer group per year. It is given that equation is cubic so let the equation be
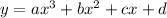 , where the scale of x- axis changes in reference taken 2002 start with 0 in graph shown in attachment.
, where the scale of x- axis changes in reference taken 2002 start with 0 in graph shown in attachment.
From the given data put the value of x and y and get the equation
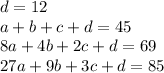
Solving these equations we get the value of a, b, c and d which are
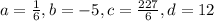
so, the equation is
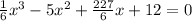
At the point of local maximum graph sudden changes it goes down, first derivative is 0. As seen in graph the point of local maximum is at he point shown in graph i.e. on the year 2007.