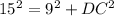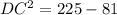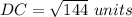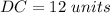Answer:
Part 1)
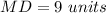
Part 2)
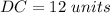
Explanation:
Step 1
Find the length of MD
we know that
The incenter is the intersection of the angle bisectors of the three vertices of the triangle. Is the point forming the origin of a circle inscribed inside the triangle
so
In this problem
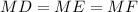 ------> is the radius of a circle inscribed inside the triangle
------> is the radius of a circle inscribed inside the triangle
we have that

therefore
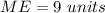
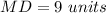
Step 2
Find the length of DC
we know that
In the right triangle MDC
Applying the Pythagoras theorem
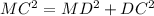
we have
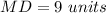
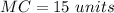
substitute