Question

Determine any point in the third quadrant for which tan(α)=4.

One valid point = ??

For this angle, sin(α) = ??

Thank you for your help!!

Answer 1

The valid point in third quadrant is (-1, -4)

For this angle,
`sin(\alpha)=(-4)/(√(17))`

Explanation:

Given that,
`tan(\alpha)= 4`

We know that,
`tan=(Opposite)/(Adjacent)`

According to the below diagram, as
`\alpha` is in third quadrant, so....

`tan(\alpha)= (AB)/(BO)=(-4)/(-1)`

That means,
`AB=-4` and
`BO= -1`

So, the coordinate of point A will be:
`(-1, -4)`

Now,
`Sin(\alpha)=(Opposite)/(Hypotenuse)=(AB)/(AO)`

Using Pythagorean theorem.......

`AO^2= AB^2+BO^2\\ \\ AO^2= (-4)^2+(-1)^2\\ \\ AO^2= 16+1=17\\ \\ AO=√(17)`

So,
`Sin(\alpha)= (AB)/(AO)= (-4)/(√(17))`

Answer 2

The point in third quadrant is: (-1,-4)

The value of sinα is
`(-4)/(√(17))`

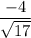
Explanation:

We are given that:

`\tan \alpha =4`

As we know that

`\tan \alpha =(P)/(B)`

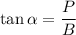
Where P denotes the perpendicular and B denote the base of a right angled triangle formed by the help of the trignometric identity.

Thus means that P=4 and B=1

Hence the hypotenuse is given by H=
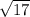`√(17)` ( with the help of Pythagorean theorem)

so we could construct a triangle in third quadrant

Hence the point in third quadrant is (-1,-4).

Now corresponding to this point
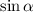`\sin \alpha` is given as:

`\sin \alpha=(P)/(H)`

⇒
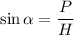
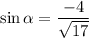`\sin \alpha=(-4)/(√(17))` (Negative sign is used as
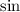`\sin` is negative in the third quadrant)