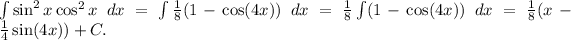Question

What is the antiderivative of sin^2(x)cos^2(x)?

Answer 1

`(x)/(8)-(\sin(4x))/(32)+C`

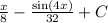
Explanation:

[Most of the work here comes from manipulating the trig to make the term (integrand) integrable.]

Recall that we can express the squared trig functions in terms of cos(2x). That is,

`\cos(2x)=2\cos^2x-1 \\ \cos(2x)=1 - 2\sin^2x.`

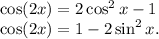
And so inverting these,

`\cos^2x=(1)/(2) (1+\cos2x) \\ \sin^2x=(1)/(2) (1-\cos2x)`.

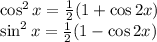Multiply them together to obtain an equivalent expression for sin^2(x)cos^2(x) in terms of cos(2x).

`\sin^2x \cdot \cos^2x =(1)/(2) (1-\cos2x) \cdot (1)/(2) (1+\cos2x) = (1)/(4)(1-\cos^2(2x)).`

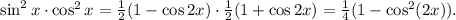
Notice we have cos^2(2x) in the integrand now. We've made it worse! Let's try plugging back in to the first identity for cos^2(2x).

`\cos(2x)=2\cos^2x-1 \Rightarrow \cos(4x)=2\cos^2(2x)-1 \Rightarrow \cos^2(2x) = (1)/(2)(1+\cos(4x))`

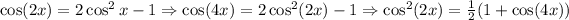
So then,

`\sin^2x \cdot \cos^2x = (1)/(4)(1-\cos^2(2x)) = (1)/(4)(1-(1)/(2)(1+\cos(4x))) = (1)/(4)(1-(1)/(2)-(1)/(2)\cos(4x))=(1)/(8)(1-\cos(4x)).`

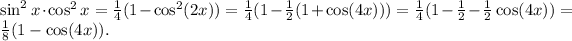
This is now integrable (phew),

`\int \sin^2x\cos^2x \ dx = \int (1)/(8)(1-\cos(4x)) \ dx = (1)/(8) \int (1-\cos(4x)) \ dx = (1)/(8)(x-(1)/(4)\sin(4x))+C.`