Answer:

Explanation:
we are given a quadratic equation
Let's assume formula of vertex form of parabola as

where vertex is (h,k)
we are given
vertex =(11,-2)
so, h=11, k=-2
now, we can plug it
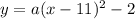
now, we are given zeros at x=10 and x=12
we know that zeros will be x=10 , y is 0
so, we can plug x=10 and y=0 and solve for 'a'
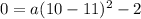

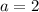
now, we can plug it back
and we get

so, we get quadratic equation as
