Answer:
Option: B is correct
Explanation:
We know that A and B represents two different school populations.
Hence, A and B will be a positive integer.
Also we are given A>B
Since,
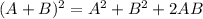
⇒
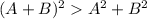 ( As 2AB is a positive quantity)
( As 2AB is a positive quantity)
Also
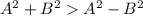
Since an positive quantity
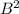 added to
added to
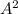 will make the term greater than an positive quantity
will make the term greater than an positive quantity
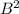 subtracted from
subtracted from
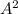 .
.
Also
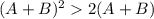
(Since
 for all n>2)
for all n>2)
Hence the largest term among all the terms is
 .
.