Question

(ar^b)^4=81r^24
where a and b are positive integers.
Work out a and b

Answer 1

Vales of a =3 and b = 6

Explanation:

Given that:
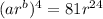`(ar^b)^4 = 81r^(24)` .....[1] where a and b are positive integers

we can write 81 and 24 as;

`81 = 3 \cdot 3 \cdot 3 \cdot 3 = 3^4`

`24 = 4 \cdot 6`

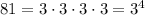
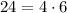
We have [1] as;

`(ar^b)^4 = 3^4r^(4 \cdot 6)`

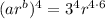
Using power rules;

`a^nb^n = (ab)^n`

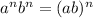
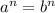`a^n = b^n` which implies a = b

then;

`(ar^b)^4 = (3r^6)^4`

`ar^b = 3r^6`

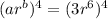
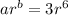
On comparing both sides we have;

a = 3 and

`r^b = r^6`

⇒
`b = 6`

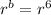
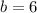
Therefore, the value of a and b are, 3 and 6