Answer:
D) None of the above
Explanation:
We are given the following expression and we are to factorize it:
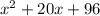
Finding factors of 96 such that they give a product of 96 when they are multiplied and 20 when they are added:
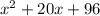
=
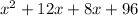
=
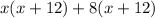
=

So the two factors of the given quadratic expression
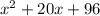 are (x + 12) and (x + 8). But these are not present in the given answer options so the correct option is D) None of the above.
are (x + 12) and (x + 8). But these are not present in the given answer options so the correct option is D) None of the above.