Question

Which of the following is a factor of 5x3 − 135?

A) 5
B) x + 3
C) x2 − 3x + 9
D) All of the above

Answer 1

The correct answer option is A) 5.

Step-by-step explanation:

We are given the following expression and we are to factorize it:

`5x^3-135`

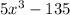
If we take the common term out of this, then we are left with:

`5(x^3-27)`

Now the term
`(x^3-27)` can also be written in the form of
`x^3-y^3` as:

`x^3-3^3`

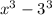
Next, we will factorize it applying the difference of cubes formula
`x^3-y^3=(x-y)(x^2+xy+y^2)` to get:

`x^3-3^2= \left(x-3\right)\left(x^2+3x+3^2\right)`

`=\left(x-3\right)\left(x^2+3x+3^2\right)`

`=\left(x-3\right)\left(x^2+3x+9\right)`

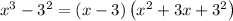
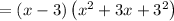
Adding the common term back to it to get:

`5\left(x-3\right)\left(x^2+3x+9\right)`

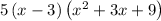
Therefore, from the given answer options we can see that the option A) 5 is the factor of the given expression 5x^3 - 135.

Answer 2

option-A

(5)

Step-by-step explanation:

we are given

`5x^3-135`

Firstly, we can factor out 5

`5x^3-5* 27`

`5(x^3-27)`

`5(x^3-3^3)`

now, we can use formula of factor

`a^3-b^3=(a-b)(a^2+ab+b^2)`

we can compare

a=x , b=3

now, we can plug this into formula

`5(x^3-3^3)=5(x-3)(x^2+3* x+3^2)`

`5(x^3-3^3)=5(x-3)(x^2+3x+9)`

so, we get

`5x^3-135=5(x-3)(x^2+3x+9)`

so, only factor 5 matches