Answer:
The correct answer option is C) 64x^2 + 40x + 25.
Explanation:
We are given the following expression:
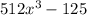
which can also be written in the form of
 as:
as:
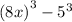
Now we will apply the difference of cubes Formula:

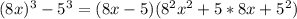
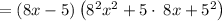
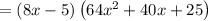
Therefore, from the given answer options we can see that the option C) 64x^2 + 40x + 25 is the factor of the given expression 512x^3 - 125.