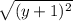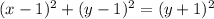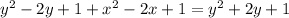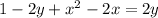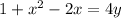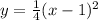Question

What is the equation of the quadratic graph with a focus of (1, 1) and a directrix of y = −1?

A) f(x) = −one fourth (x − 1)2 + 1
B) f(x) = −one fourth (x − 1)2
C) f(x) = one fourth (x − 1)2 + 1
D) f(x) = one fourth (x − 1)2

Answer 1

Answer is option D) y=
`(1)/(4)(x-1)^(2)`

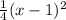
Explanation:

Quadratic graph with a focus and a directrix is a parabola as in the picture attached.

Now we assume a point (x,y) is given on the parabola.Focus of parabola be the point O(1,1) and the directrix y=(-1)

As we know that in a parabola distance OP is equal to the distance between P and directrix y=(-1)

Therefore OP = distance from directrix y = (-1)

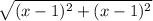`\sqrt{(x-1)^(2)+(x-1)^(2)` =
`\sqrt{(y+1)^(2)`

`(x-1)^(2) +(y-1)^(2) = (y+1)^(2)`

`y^(2)-2y+1+x^(2)-2x+1=y^(2)+2y+1`

`1-2y+x^(2)-2x=2y`

`1+x^(2)-2x=4y`

`y=(1)/(4)(x-1)^(2)`