Answer:
(c)
Explanation:
Consider ΔXBY and ΔABC
∠XYB = ∠ACB [ Corresponding angles of parallel line (AC and XY) are equal]
∠XBY = ∠ABC (Common angles)
By AA similarity, ΔXBY
 ΔABC,
ΔABC,
We know that the ratio of area of two similar triangles is the square of ratios of their sides.
Ratio of sides =
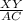
=
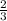
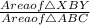 =
=
![[(XY)/(AC)]^(2)](https://img.qammunity.org/2020/formulas/mathematics/high-school/e5t2ixdj9fp5nnpef9xb63q7z2fok1s61c.png)
=
![[(3)/(2)]^(2)](https://img.qammunity.org/2020/formulas/mathematics/high-school/mrgua0d22blkp7ztp0sq8ql0zv6briar9f.png)
=
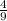
Option (c) is correct