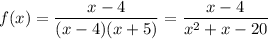If
 has a removable discontinuity at
has a removable discontinuity at
 , then the limit
, then the limit

exists and is finite.
A non-removable discontinuity at
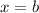 would entail a non-finite limit,
would entail a non-finite limit,
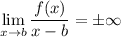
or the limit does not exist (which could be due to the limits from either side of
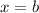 not matching or existing).
not matching or existing).
For a rational function, we want
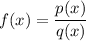
where
 and
and
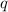 are polynomials in
are polynomials in
 . To get a removable discontinuity at
. To get a removable discontinuity at
 , both
, both
 and
and
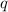 must be divisible by
must be divisible by
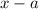 , and the limit of their quotient after removing these factors still exists. That is,
, and the limit of their quotient after removing these factors still exists. That is,
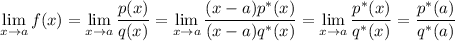
On the flip side, we get a non-removable discontinuity
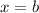 if
if
 is not divisible by
is not divisible by
 , in which case
, in which case

and this is undefined.
Suppose
 has a non-removable discontinuity at
has a non-removable discontinuity at
 and a removable one at
and a removable one at
 . Then one such function could be
. Then one such function could be