Question

An object that has a height of 0.4 meter is placed at a distance of 0.7 meter from a concave spherical mirror. An image is formed in front of the mirror and has a height of 0.35 meter. How from the mirror is the image located?

Answer 1

0.6125 meters

Step-by-step explanation:

We know that,

the height of the object (h) = 0.4 m,

the distance between the object and the mirror (u) = -0.7 m; and

the height of image (h') = 0.35 m.

For a concave spherical mirror, we know the formula of magnification:

magnification =
`(h)/(h')` =
`-(v)/(u)`

`(0.35)/(0.4) =(-v)/(-0.7)`

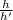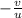
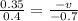
By cross multiplication:

`v=(0.35*0.7)/(0.4)`

`v= 0.6125`

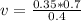
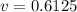
Therefore, the image is located 0.6125 meters away from the mirror.