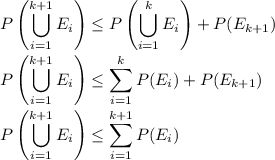The base case of
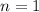 is trivially true, since
is trivially true, since
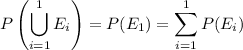
but I think the case of
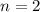 may be a bit more convincing in this role. We have by the inclusion/exclusion principle
may be a bit more convincing in this role. We have by the inclusion/exclusion principle
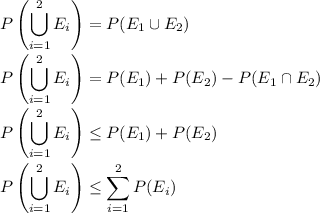
with equality if
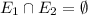 .
.
Now assume the case of
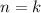 is true, that
is true, that
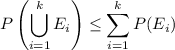
We want to use this to prove the claim for
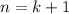 , that
, that
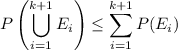
The I/EP tells us
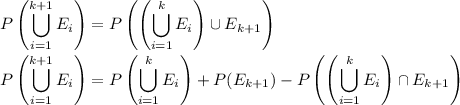
and by the same argument as in the
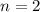 case, this leads to
case, this leads to
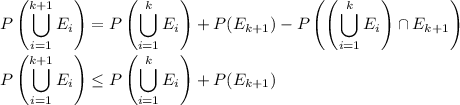
By the induction hypothesis, we have an upper bound for the probability of the union of the
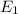 through
through
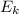 . The result follows.
. The result follows.