Question

In a Laundromat, during the spin-dry cycle of a washer, the rotating tub goes from rest to its maximum angular speed of 8.70 rev/s in 6.80 s. You lift the lid of the washer the instant the angular speed reaches the maximum value, and notice that the tub decelerates and comes to a stop in 19.0 s. Assuming that the tub rotates with constant angular acceleration while it is starting and stopping, determine the total number of revolutions undergone by the tub during this entire time interval.

Answer 1

Since we assume the accelerations are constant, the instantaneous acceleration is the same as the average acceleration, so in the first 6.80 seconds we have

`\alpha_1 = \alpha_(\rm ave) = (\Delta \omega)/(\Delta t) = (8.70(\rm rev)/(\rm s))/(6.80\,\rm s) \approx 1.28 (\rm rev)/(\mathrm s^2)`

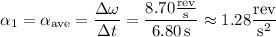
In this time, the tub undergoes an angular displacement of

`\theta_1 = \frac12 \alpha_1 (6.80\,\mathrm s)^2 \approx 29.6\,\mathrm{rev}`

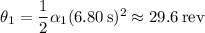
In the next 19.0 seconds the tub has acceleration

`\alpha_2 = (-8.70(\rm rev)/(\rm s))/(19.0\,\rm s) \approx -0.458 (\rm rev)/(\mathrm s^2)`

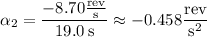
and in this time, the tube undergoes an additional displacement of

`\theta_2 = \left(8.70(\rm m)/(\rm s)\right)(19.0\,\mathrm s) + \frac12 \alpha_2 (19.0\,\mathrm s)^2 \approx 82.7\,\mathrm{rev}`

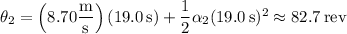
So the tub completes
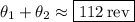`\theta_1+\theta_2 \approx \boxed{112\,\mathrm{rev}}`.