Question

In equilateral ∆ABC with side a, the perpendicular to side AB at point B intersects extension of median AM in point P. What is the perimeter of ∆ABP, if MP = b?

Answer 1

Perimeter = (2 + √3)·a

Explanation:

Given: ΔABC is equilateral and AB = a

The diagram is given below :

AM is a median , PB ⊥ AB , PM = b

Now, by using properties of equilateral triangle, median is perpendicular bisector and each angle is of 60°.

We get, ∠AMB = 90°. So, by linear pair ∠AMB + ∠PMB = 180° ⇒ ∠PMB = 90°. Also, ∠ABC = 60° and ∠ABP = 90° (given) So, ∠PBM = 30°

Since, AM is perpendicular bisector of BC. So,

`MB = (a)/(2)`

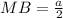
Now in ΔAMB , By using Pythagoras theorem

`AB^(2)=AM^(2)+MB^(2)\\AM^(2)=AB^(2)-MB^(2)\\AM^(2)=a^(2)-((a)/(2))^(2)\\AM=(√(3)\cdot a)/(2)`

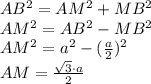
Now, in ΔBMP :

`sin\thinspace 30^(o)=\frac{\text{Perpendicular}}{\text{Hypotenuse}}\\\\sin\thinspace 30^(o)=\frac{\text{MB}}{\text{PB}}\\\\PB=\frac{\text{MB}}{\text{sin 30}}\\\\PB=((a)/(2))/((1)/(2))\implies PB = a\\\\tan\thinspace 30^(o)=\frac{\text{Perpendicular}}{\text{Base}}\\\\tan\thinspace 30^(o)=\frac{\text{MB}}{\text{PM}}\\\\PM=\frac{\text{MB}}{\text{tan 30}}\\\\PM=((a)/(2))/((1)/(\sqrt3))\implies PM=b= (√(3)\cdot a)/(2)`

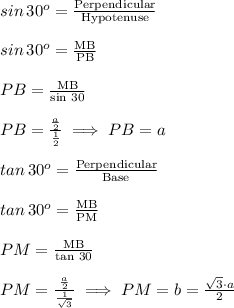
Perimeter of ABM = AB + PB + PM + AM

`\text{Perimeter = }a+a+b+ (√(3)\cdot a)/(2)\\\\=2\cdot a + (√(3)\cdot a)/(2) +(√(3)\cdot a)/(2)\\\\=2\cdot a +√(3)\cdot a\\\\=(2+\sqrt3})\cdot a`

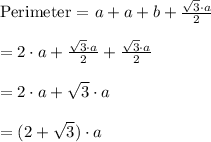
Hence, Perimeter of ΔABP = (2 + √3)·a units