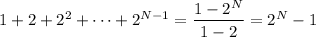These
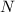 outcomes make up the entire sample space, so
outcomes make up the entire sample space, so
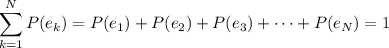
We're given that
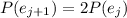 for all
for all
 , so
, so
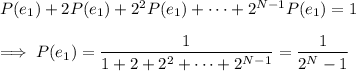
Then we can solve the recurrence relation to get the probability of the
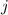 -th outcome,
-th outcome,
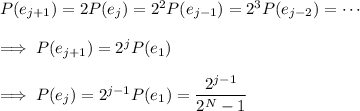
The probability of getting this sequence of
 outcomes is then
outcomes is then
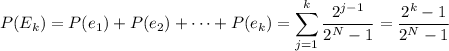
as required.
Some preliminary results: If
 is the sum of the first
is the sum of the first
 terms of a geometric series with first term
terms of a geometric series with first term
 and common ratio
and common ratio
 , then
, then
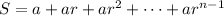
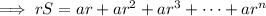
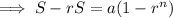
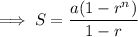
which gives us, for instance,