Question

Given n noodles in a bowl and randomly attaching ends. what is the expected number of loops you will have in the end?

Answer 1

Expected #loops:
`(1)/(2n-1)+(1)/(2n-3)+...+1`

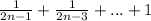
Explanation:

If there are n noodles, there are 2n ends. At the beginning, suppose you picked up a random end. The probability of randomly picking another end and that end being of the same noodle is 1/(2n-1). You get one loop, if that happens. After this step, there will only be n-1 noodles in the bowl (n-1 short non-looped noodles and 1 looped, or n-1 non-looped noodles one of which is twice as long).

Now you repeat the process. Pick a random end. The probability that the next pick will be of the same noodle is 1/(2(n-1)-1)=1/(2n-3). This repeats until there is only one noodle. Clearly, the probability that you loop that one is 1. Now to get the expected count we need to sum up all of these steps (each accounting for making one loop):

Expected #loops:
`(1)/(2n-1)+(1)/(2n-3)+...+1`

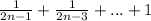
for n=10, you can expect only about 2.1 loops on average, and for n=100 only about 3.3 loops, which probably surprising to most.