Answer:
The equation of function A is
 and the equation of function B is
and the equation of function B is
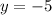 .
.
Explanation:
The point slope form of a linear function is

Where m is slope.

It is given that the function A passing through the points (–5, –2) and (–5, 7).
The equation of function A is


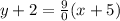
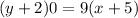
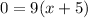
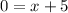

It is given that the function B passing through the points (7, –5) and (–2, –5).
The equation of function B is
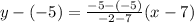
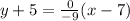
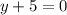
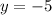
Therefore equation of function A is
 and the equation of function B is
and the equation of function B is
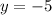 .
.