Question

"write an expression that evaluates to true if the value of the integer variable x is divisible (with no remainder) by the integer variable y. (assume that y is not zero.)"

Answer 1

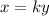`x=ky` , where k is a constant.

Explanation:

We are given that x and y are variables having integer values where y ≠ 0.

It is required to write an expression such that 'x is exactly divisible by y' i.e. there is no remainder.

Let us consider x= 12 and y = 4 ( ≠ 0 ),

Then,
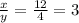`(x)/(y) =(12)/(4)=3` i.e. x = 12 is completely divisible by y = 4.

It gives the relation x = 3y and also, this relation
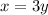`x=3y` is the true for x =12 and y =4.

Hence, the required expression is
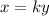`x=ky` , where k is a constant.

Answer 2

As we have to write an expression , which evaluates to true if the value of the integer variable x is divisible (with no remainder) by the integer variable y, y≠0.

so, when x is divided by y we should get remainder as 0.

Using Euclid division lemma

x= y* q + m, i.e when an integer x is divided by y gives quotient q and remainder m.

Here , m=0

So, x = q * y

So, the expression which describes the above relationship is ,

`(x)/(y)=q`, where q is Quotient.