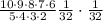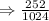1 Answer

Pavel Nikolov · Answer 1 · 2020-08-25T15:22:39+0000

Answer:

0.2460 is the required probability.

Explanation:

We have been given binomial model

n is the total number of questions which is 10

x is the questions taken out to be which is 5

p is the probability of right answers which is :
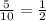
(5)/(10)=(1)/(2)

q is the probability of the false answers which is :
1-p=1-(1)/(2)=(1)/(2)

We will use the model by substituting the values we get:

P(x)=[(n!)/(x!(n-x)!)]p^xq^(n-x) on substituting the values we get:

$P(x)=[(`10!)/(5!(5)!)]\frac({1}{2})^5\cdot (1)/(2)^(5)$

$P(x)=(10\cdot9\cdot8\cdot7\cdot6\cdot5!)/(5!(5\cdot4\cdot3\cdot2\cdot1))\cdot(1)/(2)^5\cdot(1)/(2)^5$

Cancel out the common terms from numerator and denominator we get:

$(10\cdot9\cdot8\cdot7\cdot6)/(5\cdot4\cdot3\cdot2)(1)/(32)\cdot(1)/(32)$

$\Rightarrow 14\cdot18\cdot(1)/(1024)$

$\Rightarrow (14\cdot18)/(1024)$

$\Rightarrow (252)/(1024)$

$\Rightarrow 0.2460$

Please log in or register to add a comment.